| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- logarithm mapping
- PointNet++
- Slam
- OpenCV 모듈
- 코딩테스트
- OpenCV
- 백준 1253번
- point cloud
- deformable KPConv
- visual slam
- KPConv
- exponential mapping
- 부자 아빠 가난한 아빠
- rigid KPConv
- 2 포인터 알고리즘
- 제 6장
- ros2
- TURTLEBOT3
- 입문 Visual SLAM
- 코딩 테스트
- FeatureMatching
- Raspberry Pi
- SLAMKR
- Docker
- IMAGE
- 논문 리뷰
- C++
- 코딩테스트 공부
- PointNet
- 경제 공부
- Today
- Total
꿈꾸는 개발자
리 군과 리 대수(Lie Group, Lie Algebra) 본문
Visual SLAM을 공부하다 보면 리 군과 리 대수에 대한 개념을 접하게 된다.
이는 매우 어려운 개념 중 하나인데, 최근 AI Robotics KR 스터디에 참여하게 되면서 자율주행을 위한 Visual SLAM 책을 토대로 4장 리 군과 리 대수에 대한 내용을 발표하게 되어 공부한 내용을 정리해보려고 한다.
본 포스팅은 Visual SLAM에서 다루는 내용만을 가지고 공부를 했기 때문에 보다 더 넓은 군론에 대한 개념을 보고 싶다면 BC Hall 저자의 Lie Groups, Lie Algebras, and Representations를 참조하기 바란다.
목차는 다음과 같다.
- 선행 지식
- 리 군과 리 대수는 무엇일까?
- SO(3), so(3)
- SE(3), se(3)
- 지수 매핑과 로그 매핑
- 리 대수 유도 및 섭동 모델
- 유사 변환 군(Sim(3))과 리 대수(sim(3))
1. 선행 지식
리 군과 리 대수에 대한 내용을 시작하기 앞서 선행 지식이 다소 많이 필요하다.
먼저, 선형 대수에 대해 익히고 오는 것을 추천한다.
아래 내용은 리 군과 리 대수를 설명할 때 사용되는 내용에 대한 사전 정리라고 생각하면 될 것 같다.
- 3장에서 3차원 회전 행렬이 특수 직교 군(Special Orthogonal Group) SO(3)를 구성하고 변환 행렬이 특수 유클리드 군(Special Euclidean Group) SE(3)를 구성한다고 정의했었다. $ \\ $ $ \begin{align} \\ & SO(3) = \{ R \in \mathbb{R^{3x3}} | RR^{T} = I, det(R) = 1\} \\ & SE(3) = \left\{ T = \begin{bmatrix}
R & t \\
0^{T} & 1 \\
\end{bmatrix} \in \mathbb{R^{4x4}} | R \in SO(3), t \in \mathbb{R^{3}} \right \} \end{align} $ $ \\ $ - 두 행렬 모두 덧셈 연산에 대해 닫혀 있지 않지만, 곱셈 연산에는 닫혀 있다. $ \\ $ $ R_1 + R_2 \notin SO(3), \;\;\; T_1 + T_2 \notin SE(3) $ $ \\ $ $ R_1R_2 \in SO(3), \;\;\; T_1T_2 \in SE(3) $ $ \\ $
- skew-symmetric 행렬이란 행렬 $ A $가 $ A^{T} = - A $ 를 충족한다는 것을 의미한다.
- 외적 연산의 경우 $ \wedge $ 기호를 도입하여 표기하고, 임의의 벡터 $ a $에 대해 skew-symmetric 행렬 $ A $로 변환하는 의미로 사용된다.
- $ a^{\wedge} = A = \begin{bmatrix} 0 & -a _3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix}, \; A^{\vee} = a $
- 테일러 급수(Taylor series), 테일러 확장(Taylor expansion)
- $ f(x) = p_{\infty}(x) $
- $ \begin{align} p_{n}(x) & = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^{n} \\ & = \sum_{k=0}^{n} \frac{f^{(k)}(a)}{k!}(x-a)^{k} \end{align} $
- 1차 테일러 확장
- $ f(x) = f(a) + f'(a)(x-a) + Q_2(x) $
- 이때, $ Q(x) $를 0처럼 생각
- $ x $가 $ a $에 가까운 경우 근사 오차가 거의 없기 때문에 1차 테일러 확장을 위와 같이 진행할 수 있게 된다.
2. 리 군(Lie Group)과 리 대수(Lie Algebra)는 무엇일까?
리 군(Lie Group)은 연속적이고(continuous) 부드러운(smooth) 속성을 가진 군을 말한다. 정수 군과 같이 이산적인 군은 연속적인 속성이 없으므로 리 군에 속하지 않는다.
SO(n)와 SE(n)는 실수 공간에서 연속적이므로 리 군에 속한다.(강체가 공간에서 지속해서 움직일 수 있으므로 연속적이다.)
리 대수는 리 군 원점 근처의 지역적 특성을 설명하며 다른 말로는 접평면(Tangent Space)이다.
각 리 군에는 그에 상응하는 리 대수가 존재한다.
그림으로 나타내면 다음과 같다.

3. SO(3), so(3)
임의의 회전 행렬 $ R $을 이용해 리 군(SO(3))과 리 대수(so(3))간의 관계를 이해해보자
$ RR^{T} = I $
여기서 $ R $은 카메라의 회전을 나타내고, 시간에 따라 연속적으로 변경되기 때문에 시간의 함수로 나타내면 $ R(t) $로 나타낼 수 있다.
$ R(t)R(t)^{T} = I $
양 변을 시간으로 미분하면 다음과 같다.
$ \dot{R}(t)R(t)^{T} + R(t)\dot{R}(t)^{T} = 0 $
$ \dot{R}(t)R(t)^{T} = -\left ( \dot{R}(t)R(t)^{T} \right)^{T} $
$ \dot{R}(t)R(t)^{T} $ 는 skew-symmetric 행렬임을 알 수 있다.
따라서 $ \wedge $ 기호를 이용해 $ \phi(t) \in \mathbb{R}^{3} $ 에 해당하는 3차원 벡터를 찾을 수 있다.
$ \dot{R}(t)R{t}^{T} = \phi(t)^{\wedge} $
양 쪽에 $ R(t) $를 곱하면 다음과 같다.
$ \dot{R}(t) = \phi(t)^{\wedge}R(t) = \begin{bmatrix} 0 & -\phi_3 & \phi_2 \\ \phi_3 & 0 & -\phi_1 \\ -\phi_2 & \phi_1 & 0 \end{bmatrix} $ $ R(t) $
이로써 회전 행렬의 미분을 구하기 위해선 회전 행렬의 왼쪽에 $ \phi(t)^{\wedge} $를 곱하면 된다.
$ t_0 = 0 $ 일 때, 회전 행렬 $ R(0) = I $로 설정한 후 $ R(t) $를 $ t = t_0 $ 근처에서 1차 테일러 확장을 수행하면 다음과 같다.
$ \begin{align} R(t) & \approx R(t_0) + \dot{R}(t_0)(t - t_0) \\ & = I + \phi(t_0)^{\wedge}(t) \end{align} $
$ \phi $가 SO(3) 원점 근처의 접평면에 위치한다는 것으로 다음과 같이 식이 전개된다.
$ \dot{R}(t) = \phi(t_0)^{\wedge}R(t) = \phi^{\wedge}_{0}R(t) $
따라서, 위 방정식은 $ R $에 대한 미분 방정식이며 초깃값은 $ R(0) = I $ 이고, 방정식의 해는 $ \phi(t_0) = \phi_0 $로 다음과 같이 나타낼 수 있다.
$ R(t) = exp(\phi^{\wedge}_0t) $
시간에 대한 내용을 제외한다면 다음과 같다.
$ R = exp(\phi^{\wedge}) $
이는 회전 행렬 $ R $이 지수 관계를 통해 행렬 $ \phi^{\wedge} $ 라는 또 다른 skew-symmetric 행렬로 나타낼 수 있다는 뜻이다.
여기서 $ \phi $를 SO(3)에 해당하는 리 대수 so(3)라고 말한다.
$ so(3) = \left\{ \phi \in \mathbb{R^{3}}, \Phi = \phi^{\wedge} \in \mathbb{R^{3x3}} \right\} $
4. SE(3), se(3)
SE(3) 또한 대응하는 리 대수 se(3)가 존재한다.
임의의 변환 행렬 $ g $를 이용해 리 군(SE(3))과 리 대수(se(3))간의 관계를 이해해보자
임의의 변환 행렬 $ g $를 시간에 따라 연속적으로 변하기 때문에 시간에 대한 함수로 변형시키면 다음과 같이 나타낼 수 있다.
$ \begin{align} g(t) = \begin{pmatrix} R(t) & T(t) \\ 0 & 1 \end{pmatrix} \end{align} $
$ g $의 역행렬은 다음과 같이 정의된다.
$ \begin{align} g^{-1}(t) = \begin{pmatrix} R(t)^{T} & -R(t)^{T}T(t) \\ 0 & 1 \end{pmatrix} \end{align} $
$ g(t) $를 미분하면 다음과 같다.
$ \begin{align} \dot{g}(t) = \begin{pmatrix} \dot{R}(t) & \dot{T}(t) \\ 0 & 0 \end{pmatrix} \end{align} $
특수 직교 군에서 진행했던 것처럼 미분 방정식으로 exponential mapping이 가능한 지 확인하기 위해 다음과 같이 진행한다.
$ \begin{align} \dot{g}(t)g^{-1}(t) & = \begin{pmatrix} \dot{R}(t) & \dot{T}(t) \\ 0 & 0 \end{pmatrix} \begin{pmatrix} R(t)^{T} & -R(t)^{T}T(t) \\ 0 & 1 \end{pmatrix} \\ & = \begin{pmatrix} \dot{R}(t)R^{T}(t) & \dot{T}(t) - \dot{R}(t)R^{T}(t)T(t) \\ 0 & 0 \end{pmatrix} \\ & = \begin{pmatrix} \phi^{\wedge}(t) & \rho(t) \\ 0 & 0 \end{pmatrix}, \because \dot{R}(t)R^{T}(t) = \phi^{\wedge}(t), \,\, \dot{T}(t)-\dot{R}(t)R^{T}(t)T(t) = \rho(t) \end{align} $
$ \therefore \begin{align} \dot{g}(t)g^{-1}(t) = \begin{pmatrix} \phi^{\wedge}(t) & \rho(t) \\ 0 & 0 \end{pmatrix} = \xi^{\wedge}(t) \end{align} $
위 식에서의 $ \xi $는 6차원 벡터를 의미하고 $ \xi $ 에서 사용되는 $ \wedge $ 연산은 skew symmetric 행렬 변환을 의미하지 않고, 6차원 벡터를 4차원 행렬로 변환하는 의미로 사용된다.
양 변에 $ g(t) $를 곱하면 다음과 같다.
$ \begin{align} \dot{g}(t) = \xi^{\wedge}(t) g(t) \end{align} $
$ g(t) $에 대한 미분 방정식이며 시간에 대한 내용을 제외한다면 다음과 같다.
$ \therefore g = exp(\xi^{\wedge}) $
이는 변환 행렬 $ g $가 지수 관계를 통해 행렬 $ \xi^{\wedge} $ 라는 또 다른 4차원 행렬로 나타낼 수 있다는 뜻이다.
여기서 $ \xi $를 SE(3)에 해당하는 리 대수 se(3)라고 말한다.
$ \begin{align} se(3) = \left\{ \xi = \begin{bmatrix} \rho \\ \phi \end{bmatrix} \in \mathbb{R^{6}}, \rho \in \mathbb{R^{3}}, \phi \in so(3), \xi^{\wedge} = \begin{bmatrix} \phi^{\wedge} & \rho \\ 0^{T} & 0 \end{bmatrix} \in \mathbb{R^{4x4}} \right\} \end{align} $
5. 지수 매핑과 로그 매핑
1) SO(3), so(3)의 지수 매핑(so(3) -> SO(3))
임의의 행렬 지수가 수렴될 경우, 테일러 급수를 통해 다음과 같이 나타낼 수 있다.
$ \begin{align} exp(A) = \sum_{n=0}^{\infty} \frac{1}{n!}A^{n} \end{align} $
$ \begin{align} exp(\phi^{\wedge}) = \sum_{n=0}^{\infty} \frac{1}{n!}(\phi^{\wedge})^{n} \end{align}, \;\;\;\, \because A = \phi^{\wedge} $
행렬의 무한 거듭 제곱 계산을 진행할 수 없기 때문에, $ \phi $는 3차원 벡터라는 특성을 이용해 길이와 방향을 각각 $ \theta, a $으로 표현함으로써 $ \phi = \theta a$으로 행렬의 무한 거듭 제곱 계산을 우회하여 계산한다.
여기서 $ a $은 길이가 1인 단위 방향 벡터로 $ ||a|| = 1 $이고, 두 가지 특성이 존재한다.(직접 계산해보면 쉽게 이해가 가능하다)
- $ a^{\wedge}a^{\wedge} = \begin{bmatrix} -a^2_2 - a^2_3 & a_1a_2 & a_1a_3 \\ a_1a_2 & -a^2_1 - a^2_3 & a_2a_3 \\ a_1a_3 & a_2a_3 & -a^2_1 - a^2_2 \end{bmatrix} = aa^{T} - I $
- $ a^{\wedge}a^{\wedge}a^{\wedge} = a^{\wedge}(aa^{T} - I) = -a^{\wedge} $
위 두 특성을 이용하면 $ a^{\wedge} $ 고차 항에 대해 계산할 수 있으며 이를 이용해 지수 매핑을 다음과 같이 계산할 수 있다.
$ \begin{align} exp(\phi^{\wedge}) & = exp(\theta a^{\wedge}) = \sum_{n=0}^{\infty} \frac{1}{n!} (\theta a^{\wedge})^{n} \\ & = I + \theta a^{\wedge} + \frac{1}{2!}\theta^{2}a^{\wedge}a^{\wedge} + \frac{1}{3!}\theta^{3}a^{\wedge}a^{\wedge}a^{\wedge} + \frac{1}{4!}\theta^{4}(a^{\wedge})^{4} + \cdots \\ & = aa^{T} - a^{\wedge}a^{\wedge} + \theta a^{\wedge} + \frac{1}{2!}\theta^{2}a^{\wedge}a^{\wedge} - \frac{1}{3!}\theta^{3}a^{\wedge} - \frac{1}{4!}\theta^{4}(a^{\wedge})^{2} + \cdots \\ & = aa^{T} + \underbrace{ \left( \theta - \frac{1}{3!}\theta^{3} + \frac{1}{5!}\theta^{5} - \cdots \right) }_{sin \theta} a^{\wedge} - \underbrace{\left(1 - \frac{1}{2!}\theta^{2} + \frac{1}{4!}\theta^{4} - \cdots \right) }_{cos \theta} a^{\wedge}a^{\wedge} \\ & = a^{\wedge}a^{\wedge} + I + sin\theta a^{\wedge} - cos\theta a^{\wedge}a^{\wedge} \\ & = (1 - cos\theta)a^{\wedge}a^{\wedge} + I + sin\theta a^{\wedge} \\ & = cos\theta I + (1 - cos\theta)aa^{T} + sin\theta a^{\wedge} \end{align} $
최종적으로 로드리게스 식과 같은 식이 됨을 알 수 있다. 따라서 로드리게스 식을 통해 so(3)의 모든 벡터를 SO(3)의 회전 행렬에 매핑할 수 있다.
2) SO(3), so(3)의 로그 매핑(SO(3) -> so(3))
회전 행렬에서 회전 벡터로의 변환은 3장에서 배웠다.
이를 이용해 리 군에서 리 대수로의 로그 매핑을 알 수 있다.
$ \begin{align} tr(R) & = cos\theta \; tr(I) + (1 - cos\theta)tr(aa^{T}) + sin\theta \; tr(a^{\wedge}) \\ & = 3cos\theta + (1 - cos\theta) \\ & = 1 + 2cos\theta \end{align} $
$ \begin{align} \therefore \theta = arccos \frac{tr(R) - 1}{2} \end{align} $
단위 방향 벡터는 회전 후에도 변경되지 않는다.
$ Ra = a $
최종적으로 3차원 회전 행렬(SO(3)) 3차원 회전 벡터(so(3))로 변환하는 로그 매핑의 수식은 다음과 같다.
$ \begin{align} & \theta = arccos \frac{tr(R) - 1}{2} \\ & Ra = a \end{align} $
3) SE(3), se(3)의 지수 매핑(se(3) -> SE(3))
$ exp(\xi^{\wedge}) $ 에 대해 테일러 급수를 통해 지수 매핑을 계산할 수 있다.
$ \begin{align} exp(\xi^{\wedge}) & = exp \begin{bmatrix} \phi^{\wedge} & \rho \\ 0 & 0 \end{bmatrix} \\ & = I + \begin{bmatrix} \phi^{\wedge} & \rho \\ 0^{T} & 0 \end{bmatrix} + \frac{1}{2!} \begin{bmatrix} (\phi^{\wedge})^{2} & \phi^{\wedge}\rho \\ 0^{T} & 0 \end{bmatrix} + \frac{1}{3!} \begin{bmatrix} (\phi^{\wedge})^{3} & (\phi^{\wedge})^{2}\rho \\ 0^{T} & 0 \end{bmatrix} + \cdots \\ & = \begin{bmatrix} \sum_{n=0}^{\infty} \frac{1}{n!} (\phi^{\wedge})^{n} & \sum_{n=0}^{\infty} \frac{1}{(n+1)!}(\phi^{\wedge})^{n}\rho \\ 0^{T} & 1 \end{bmatrix} \\ & = \begin{bmatrix} exp(\phi^{\wedge}) & J\rho \\ 0^{T} & 1 \end{bmatrix}, \;\, \because J = \sum_{n=0}^{\infty} \frac{1}{(n+1)!}(\phi^{\wedge})^{n} \\ & \triangleq \begin{bmatrix} R & J\rho \\ 0^{T} & 1 \end{bmatrix} = T \end{align} $
위 식에서 Jacobian 행렬 $ J $가 지수 매핑된 후 병진(translation) 부분에 곱해지는 것을 볼 수 있다.
$ \begin{align} \sum_{n=0}^{\infty} \frac{1}{(n+1)!}(\phi^{\wedge})^{n} & = I + \frac{1}{2!}\theta a^{\wedge} + \frac{1}{3!}(\theta)^{2} (a^{\wedge})^{2} + \cdots \\ & = \frac{1}{\theta}(1 - cos\theta)(a^{\wedge}) + \frac{\theta - sin\theta}{\theta} (aa^{T} - I) + I \\ & = \frac{sin\theta}{\theta}I + \begin{pmatrix} 1 - \frac{sin\theta}{\theta} \end{pmatrix} aa^{T} + \frac{1 - cos\theta}{\theta}a^{\wedge} \overset{\underset{\mathrm{def}}{}}{=} J \end{align} $
4) SE(3), se(3)의 로그 매핑(SE(3) -> se(3))
변환 행렬 T에 따라 so(3)에 해당하는 벡터를 찾는 것이 더 효율적으로 로그 매핑을 주로 사용하진 않지만, 다음과 같이 나타낼 수 있다.SO(3) 로그 매핑을 이용하여 회전 행렬 R에 대한 내용은 동일하고, 병진에 대한 내용만 추가된다.
$ t = J\rho $
$ J $는 $ \phi $로부터 얻을 수 있으므로 $ \rho $는 선형 방정식으로 풀 수 있게 된다.
최종적으로 SO(3), SE(3)와 so(3), se(3)에 지수 매핑과 로그 매핑에 대한 결과를 그림으로 나타내었다.
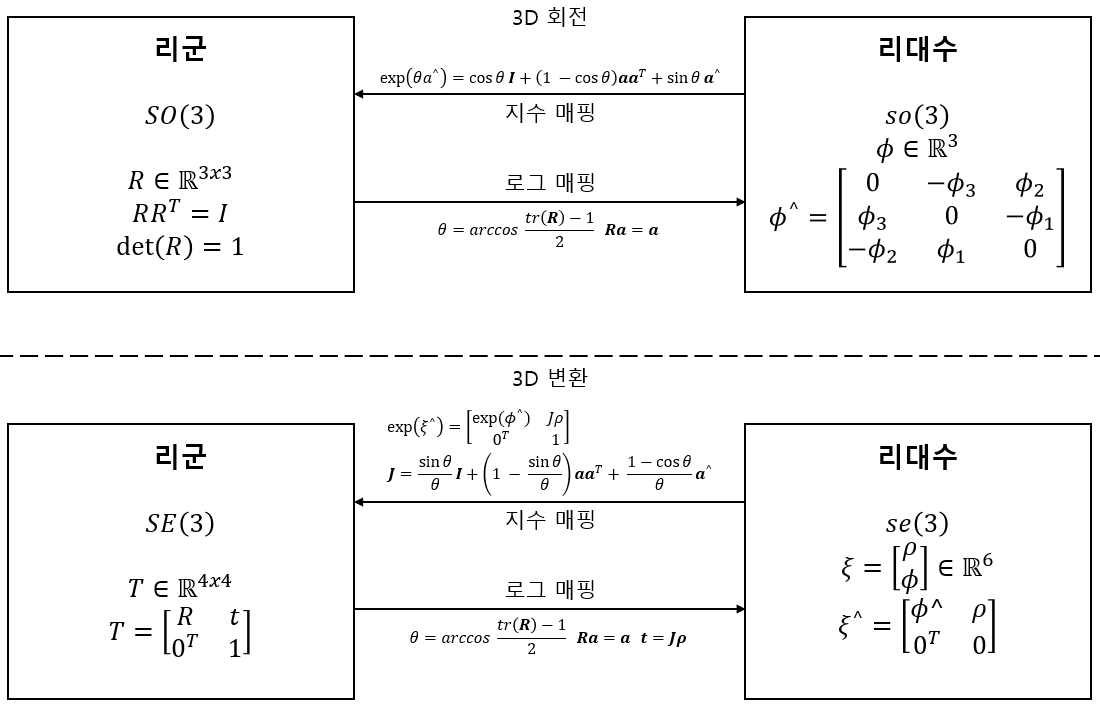
6. 리 대수 유도 및 섭동 모델
1) BCH 수식 및 근사치
SO(3)에서 두 행렬 곱을 진행하면 리 대수에서는 어떻게 계산할 수 있을까?
$ exp(\phi^{\wedge}_1)exp(\phi^{\wedge}_2) = exp((\phi_1 +\phi_2)^{\wedge}) ? $
- $ \phi_1, \; \phi_2 $ 가 스칼라인 경우라면 True
- 그러나 행렬의 지수 매핑이므로 False
우리는 이러한 계산을 Baker-Campbell-Hausdorff 수식(BCH 수식)을 사용해 근사시킬 수 있다.
BCH 수식은 다음과 같다.
$ \begin{align} ln(exp(A) exp(B)) = A + B + \frac{1}{2} [A, B] + \frac{1}{12} [ A, [A, B]] - \frac{1}{12} [B, [A, B]] + \cdots \end{align} $
- $ [A, B] = AB - BA $
$ \begin{align} ln(exp(\phi^{\wedge}_1)exp(\phi^{\wedge}_2)^{\vee} \approx \left\{ \begin{matrix} J_l(\phi_2)^{-1}\phi_1 + \phi_2 : \phi_1 이 \;\; 작은 \;\; 경우, \\ J_r(\phi_1)^{-1}\phi_2 + \phi_1 : \phi_2 이 \;\; 작은 \;\; 경우. \end{matrix} \right. \end{align} $
$ J_l $ 과 $ J_r $은 왼쪽 곱셈 오른쪽 곱셈을 나타내며, BCH 근사치에서 리 대수는 어떤 곱셈 모델(왼쪽 곱셈 또는 오른쪽 곱셈)을 사용하는 지 알고 있어야 한다.
책에서 왼쪽 곱셈 모델에 대해 설명을 진행하기 때문에 본 포스팅에서도 왼쪽 곱셈 모델($ J_l $)을 기준으로 설명한다.
자코비안 $ J_l $은 SE(3), se(3)의 지수 매핑에서 보았던 자코비안과 동일하다.
$ \begin{align} J_l = J = \frac{sin\theta}{\theta}I + \begin{pmatrix} 1 - \frac{sin\theta}{\theta} \end{pmatrix} aa^{T} + \frac{1 - cos\theta}{\theta}a^{\wedge} \end{align} $
$ \begin{align} J^{-1}_{l} = \frac{\theta}{2}cot\frac{\theta}{2}I + \begin{pmatrix} 1 - \frac{\theta}{2}cot\frac{\theta}{2} \end{pmatrix}aa^{T} - \frac{\theta}{2}a^{\wedge} \end{align} $
오른쪽 곱셈 모델의 경우 왼쪽 곱셈 모델에 마이너스 기호만 붙이면 된다.
$ J_r(\phi) = J_l(-\phi) $
따라서, 회전 행렬 $ R $의 리 대수가 $ \phi $라고 가정할 때, 왼쪽 곱셈 모델을 이용해 작은 회전에 해당하는 리 대수 $ \Delta \phi$ 를 곱해주면 다음과 같이 설명될 수 있다.
$ \begin{align} exp(\Delta \phi^{\wedge}) exp(\phi^{\wedge}) = exp((\phi + J^{-1}_l(\phi)\Delta \phi)^{\wedge}) \end{align} $
위 내용은 리 군에서 곱셈 연산을 할 경우 리 대수에서 BCH를 통해 덧셈으로 근사화 시킬 수 있는 내용이고, 아래는 리 대수에서 덧셈에 대한 연산을 할 경우 리 군에서 곱셈으로 어떻게 근사화 되는 지 나타낸 것이다.
$ \begin{align} exp((\phi + \Delta \phi)^{\wedge}) = exp((J_l \Delta \phi)^{\wedge}) exp(\phi^{\wedge}) = exp(\phi^{\wedge}) exp((J_r \Delta \phi)^{\wedge}) \end{align} $
SE(3)에 대한 BCH 근사치도 존재하나, 여기서는 생략한다.
2) 리 대수 미분 모델
SLAM에서 최적화 문제를 해결할 때, 회전 및 변환에 대한 내용을 어떻게 최적화 할 것인지에 대한 내용을 다룬다.
SO(3)의 회전 행렬과 Transformation의 변환 행렬을 이용한다.
$ z = Tp + w $
여기서 $ w $는 임의의 노이즈를 나타내고, $ z $는 관측 값을 나타낸다.
이때, 노이즈의 존재 때문에 실제 값($ z_{gt} = Tp $)과 관찰 모델 $ z $이 같을 수 없기에 오류를 최소화하는 방식으로 최적화를 진행한다.
오류에 대한 수식은 다음과 같다.
$ e = z - Tp $
만약, N개의 랜드마크의 관측 값이 있다고 가정하면, 자세 추정은 전체 오류를 최소화하는 최적의 T(변환 행렬)을 찾는 것이므로 다음과 같이 나타낼 수 있다.
$ \begin{align} \min_{T}J(T) = \sum_{i=1}{N} ||z_i - Tp_i ||^{2}_2 \end{align} $
$ J(T) $라는 목적 함수의 미분을 계산하는 방식으로 최적화 문제를 해결해나간다.
그러나, SO(3) 및 SE(3)에는 잘 정의된 덧셈 연산이 없으므로 미분을 일반적인 형식으로 정의할 수 없기에 리 대수의 관점에서 미분 문제를 해결한다.
SO(3)의 경우 점 $ p $를 회전시켜 $ Rp $를 얻었다고 가정하고, 회전 후 회전에 의한 점 좌표의 미분을 계산하기 위해 비공식적으로 다음과 같이 나타낼 수 있다.
$ \begin{align} \frac{\partial(Rp)}{\partial R} \end{align} $
SO(3)는 덧셈 연산이 없으므로, 일반적인 미분 정의에 의해 계산될 수 없기 때문에 이를 리 대수 $ \phi $로 표현하여 계산을 진행한다.
$ \begin{align} \frac{\partial(exp(\phi^{\wedge})p)}{\partial \phi} & = \lim_{\delta\phi \rightarrow 0} \frac{exp((\phi + \delta\phi)^{\wedge}p - exp(\phi^{\wedge})p}{\delta\phi} \\ & = \lim_{\delta\phi \rightarrow 0} \frac{exp((J_l\delta\phi)^{\wedge})exp(\phi)^{\wedge}p - exp(\phi^{\wedge})p}{\delta\phi} \\ & = \lim_{\delta\phi \rightarrow 0} \frac{(I + (J_l\delta\phi)^{\wedge})exp(\phi^{\wedge})p - exp(\phi^{\wedge})p}{\delta\phi} \\ & = \lim_{\delta\phi \rightarrow 0} \frac{ (J_l\delta\phi)^{\wedge}exp(\phi^{\wedge})p}{\delta\phi} \\ & = \lim_{\delta\phi \rightarrow 0} \frac{- (exp(\phi^{\wedge})p)^{\wedge}J_l\delta\phi}{\delta\phi} = -(Rp)^{\wedge}J_l \end{align} $
위 식에서 최종적으로 $ J_l $가 존재하므로, 계산이 어렵다.
이를 조금 더 쉽게 계산하기 위해 섭동 모델을 이용한 미분 계산을 진행한다.
4) 섭동 모델
섭동(perturbation) : 수학과 물리학에서 섭동 이론(perturbation theory, 攝動理論) 또는 미동 이론(微動理論)은 해석적으로 풀 수 없는 문제의 해를 매우 작다고 여길 수 있는 매개변수들의 테일러 급수로 나타내는 이론이다. 매개변수들이 매우 작으므로, 급수의 유한개의 항을 계산하여 근사적인 해를 얻을 수 있다. (출처 : 위키백과)
리 대수 미분 모델 중 SO(3)에 대한 내용에서 최종적인 계산에서 $ J_l $이 남아 계산이 어렵다는 단점이 존재했다.
이를 회전 행렬 $ R $에 대해 섭동을 추가함으로써 왼쪽 곱셈 혹은 오른쪽 곱셈 모델을 사용할 수 있게되고 이로부터 $ J_l $이 없는 최종적인 결과가 나오도록 미분 모델을 설계한 것이 특징이다.
책에서는 왼쪽 섭동 $ \Delta R $에 해당하는 리 대수를 $ \varphi $라 하고 계산을 진행한다.
$ \begin{align} \frac{\partial(Rp)}{\partial \varphi} & = \lim_{\varphi \rightarrow 0} \frac{exp(\varphi^{\wedge})exp(\phi^{\wedge})p - exp(\phi^{\wedge})p}{\varphi} \\ & = \lim_{\varphi \rightarrow 0} \frac{(I + \varphi^{\wedge})exp(\phi^{\wedge})p - exp(\phi^{\wedge})p}{\varphi} \\ & = \lim_{\varphi \rightarrow 0} \frac{\varphi^{\wedge}Rp}{\varphi} = \lim_{\varphi \rightarrow 0} \frac{-(Rp)^{\wedge}\varphi}{\varphi} = -(Rp)^{\wedge} \end{align} $
이와 같이 섭동을 이용해 미분 모델을 계산하면 자코비안이 생략되기 때문에 실용적으로 변한다.
SE(3)도 이와 같이 섭동 모델을 사용해 연산을 수행할 수 있다.
$ \begin{align} \frac{\partial\delta\xi}{\partial (Tp)} & = \lim_{\delta\xi \rightarrow 0} \frac{exp(\delta\xi^{\wedge})exp(\xi^{\wedge})p - exp(\xi^{\wedge})p}{\delta\xi} \\ & = \lim_{\delta\xi \rightarrow 0} \frac {(I+\delta\xi^{\wedge})exp(\xi^{\wedge})p - exp(\xi^{\wedge})p}{\delta\xi} \\ & = \lim_{\delta\xi \rightarrow 0} \frac{\delta\xi^{\wedge}exp(\xi^{\wedge})p}{\delta\xi} \\ & = \lim_{\delta\xi \rightarrow 0} \frac{\begin{bmatrix} \delta\phi^{\wedge} & \delta\rho \\ 0^{T} & 0 \end{bmatrix} \begin{bmatrix} Rp+t \\ 1 \end{bmatrix}}{\delta\xi} \\ & = \lim_{\delta\xi \rightarrow 0} \frac{\begin{bmatrix} \delta\phi^{\wedge}(Rp+t) + \delta\rho \\ 0^{T} \end{bmatrix}}{\left[ \delta\rho, \delta\phi \right]^{T}} = \begin{bmatrix} I & -(Rp + t)^{\wedge} \\ 0^{T} & 0^{T} \end{bmatrix} \overset{\underset{\mathrm{def}}{}}{=} (Tp)^{\bigodot} \end{align} $
7. 유사 변환 군(Sim(3))과 리 대수(sim(3))
단안 카메라에서 사용되는 유사 변환 군 Sim(3)와 해당하는 리 대수 sim(3)에 대해 설명한다.
스테레오 카메라 혹은 Depth 카메라를 사용하는 경우 이 절은 건너뛰어도 된다.
단안 SLAM에서는 일반적으로 스케일 계수를 명시적으로 표현한다.
수학적으로 3차원 공간 상의 점 p에 대해서 Euclidean transform 대신 유사 변환(Similarity Transform)이 수행된다.
이때, 스케일을 $ s $로 표현한다.
$ \begin{align} p' = \begin{bmatrix} sR & t \\ 0^{T} & 1 \end{bmatrix}p = sRp + t \end{align} $
따라서 SE(3)가 아닌 Sim(3) 행렬 곱셈 군이 형성된다.
$ \begin{align} Sim(3) = \begin{Bmatrix} S = \begin{bmatrix} sR & t \\ 0^{T} & 1 \end{bmatrix} \in \mathbb{R^{4x4}} \end{Bmatrix} \end{align} $
SO(3), SE(3)와 동일하게 해당하는 리 대수, 지수 매핑, 로그 매핑 등이 있다.
리 대수 sim(3)로는 7차원 벡터 $ \zeta $ 를 사용한다. 7차원에는 기존 6차원인 se(3)와 동일하며 스케일을 의미하는 $ \sigma $가 존재한다.
$ \begin{align} sim(3) = \begin{Bmatrix} \zeta|\zeta = \begin{bmatrix} \rho \\ \phi \\ \sigma \end{bmatrix} \in \mathbb{R^{7}}, \zeta^{\wedge} = \begin{bmatrix} \sigma I + \phi^{\wedge} & \rho \\ 0^{T} & 0 \end{bmatrix} \in \mathbb{R^{4x4}} \end{Bmatrix} \end{align} $
지수 매핑은 다음과 같다.
$ \begin{align} exp(\zeta^{\wedge}) = \begin{bmatrix} e^{\sigma}exp(\phi^{\wedge}) & J_s\rho \\ 0^{T} & 1 \end{bmatrix} \end{align} $
여기서 $ J_s $는 다음과 같다.
$ \begin{align} J_s = \frac{e^{\sigma} - 1}{\sigma}I + \frac{\sigma e^{\sigma}sin\theta + (1 - e^{\sigma}cos\theta)\theta}{\sigma^{2} + \theta^{2}}a^{\wedge} + \begin{pmatrix} \frac{e^{\sigma} - 1}{\sigma} - \frac{(e^{\sigma}cos\theta - 1)\sigma + (e^{\sigma}sin\theta)\theta}{\sigma^{2} + \theta^{2}} \end{pmatrix}a^{\wedge}a^{\wedge} \end{align} $
리 대수 $ \zeta $의 경우 대응되는 리 군은 다음과 같다.
$ \begin{align} s = e^{\sigma}, \;\; R = exp(\phi^{\wedge}), \;\; t = J_s\rho \end{align} $
Sim(3)의 섭동 모델에 대해서 SE(3)와 BCH 근사치가 유사하므로 책에서는 결과만 제공한다.
왼쪽 곱셈 모델로 나타내었고, 작은 섭동 $ exp(\zeta^{\wedge}) $를 곱하는 방식으로 섭동 모델을 계산한 결과는 다음과 같다.
$ \begin{align} \frac{\partial Sp}{\partial \zeta} = \begin{bmatrix} I & -q^{\wedge} & q \\ 0^{T} & 0^{T} & 0 \end{bmatrix} \end{align} $
본 포스팅에서는 리 군과 리 대수에 대한 내용을 알아보았고, SO(3), SE(3), Sim(3) d에 대한 섭동 모델을 알아보았다.
수학적으로 어려운 내용이 포함되어 이해가 힘들었지만, 책의 4장 내용을 정리하자면 결론은 다음과 같다.
결론
1. 리 군은 연속적이고 부드러운 속성을 가진 군이다.
2. 리 대수는 리 군 원점 근처의 지역적 특성을 설명하며 다른 말로는 접평면(Tangent Space)이다.
3. SLAM에서 리 군(SO(3), SE(3), Sim(3))과 리 대수(so(3), se(3), sim(3))는 지수 매핑과 로그 매핑을 통해 변환이 가능하다.
4. SLAM에서 최적화를 진행할 때 에러를 최소화하는 최적의 T(transformation)를 구하는 것을 목적으로 진행하는데, 이때 T는 리 군으로 덧셈 연산에 대해 정확하게 정의되지 않아 미분을 일반적인 형식으로 정의할 수 없다. 따라서, 리 대수로 변환해 최적의 T에 해당하는 리 대수를 찾고 해당 값을 리 군으로 변환함으로써 최적화를 수행한다.
- 이때 사용되는 개념 중 섭동이라는 개념을 이용해 BCH 수식으로 미분 모델의 결과에 자코비안 곱셈이 생략된 보다 실용적인 결과를 도출함으로써 계산량을 줄이는 방식을 사용한다.
5. Sim(3)에는 단안 카메라를 이용한 SLAM을 할 때 사용되고, SE(3) 보다 스케일에 대한 정보가 하나 더 추가된다.
참조 글
[SLAM] 2.리군, 리대수(Lie Group, Lie Algebra)
안녕하세요. 후니대디입니다. Lie Group, Lie Algebra에 대해서 포스팅하겠습니다. Lie라는 이름이 지어진 이유는 Lie Group에 대한 이론을 정립한 수학자 이름이 Sophus Lie이기 때문입니다. 리군,리대수는
jaehoon-daddy.tistory.com
- 자율주행을 위한 비주얼 슬램 (저자 :가오시앙 , 장타오 저자(글) · 김필은 번역) 지니북스
'SLAM' 카테고리의 다른 글
| 입문 Visual SLAM 제 6장 실습 코드 중국어 주석 번역 (0) | 2022.12.05 |
|---|---|
| 입문 Visual SLAM 제 5장 실습 코드 중국어 주석 번역 (2) | 2022.12.01 |
| 입문 Visual SLAM 제 4장 실습 코드 중국어 주석 번역 (0) | 2022.12.01 |
| 입문 Visual SLAM 제 3장 공부 (0) | 2022.11.29 |
| SLAM 개발자를 위한 공부 - 1 (0) | 2022.10.24 |




